Disclaimer
Postingan ini sepenuhnya berasal dari artikel Anda Boleh Berbohong Sekali! - Oleh Pak Aleams Barra (url: aleamsbarra.com/2016/06/01/9/). Pada tanggal terbitnya postingan ini (11/Sept/2022) url tersebut sudah tidak dapat diakses begitupun untuk domainnya (aleamsbarra.com). Oleh karena itu, postingan ini hadir untuk menyampaikan kebermanfaatan artikel tersebut tanpa mengklaim maupun mengkomersilkannya (ads). Apabila pihak yang bersangkutan tidak berkenan, mohon hubungi mimin yaa, thank you.
Permainan Menebak Angka
Wati dan Budi memainkan permainan tebak angka. Wati meminta Budi untuk memikirkan suatu angka dari 0 sampai dengan 15. Untuk bisa menebak angka ini, Budi diminta menjawab tujuh pertanyaan berikut dengan jawaban ya atau tidak. Budi diperbolehkan berbohong paling banyak satu kali ketika menjawab.
Tujuh pertanyaan yang Wati ajukan, semuanya berbentuk: apakah bilangan yang kamu pikirkan ada dihimpunan $\text{A}$ ? dengan himpunan $\text{A}$ berturut-turut adalah ketujuh himpunan berikut:
- $\{8,9,10,11,12,13,14,15\}$
- $\{4,5,6,7,12,13,14,15\}$
- $\{2,3,6,7,10,11,14,15\}$
- $\{1,3,5,7,9,11,13,15\}$
- $\{1,2,5,6,8,11,12,15\}$
- $\{1,2,4,7,9,10,12,15\}$
- $\{1,3,4,6,8,10,13,15\}$
Jawaban Budi dari ketujuh pertanyaan di atas adalah: ya, ya, ya, ya, tidak, tidak, ya. Setelah mencoret-coret sesuatu di kertas, satu menit berikutnya Wati mengumumkan bahwa Budi telah berbohong ketika menjawab pertanyaan ketiga dan angka yang dipikirkan Budi adalah 13! Budi membenarkan apa yang dikatakan Wati.
Karena merasa penasaran Budi ingin mencobanya sekali lagi. Setelah memikirkan suatu angka, berikut adalah jawaban Budi atas pertanyaan-pertanyaan yang sama seperti pada permainan yang pertama: tidak, ya, tidak, tidak, ya, tidak, tidak. Bisakah anda membantu Wati untuk menebak apa angka yang dipikirkan Budi?
Solusi Wati
Berikut adalah cara Wati untuk menentukan bilangan apa yang dipikirkan Budi. Untuk setiap jawaban Budi, Wati menuliskan angka 1 jika Budi menjawab ya dan 0 jika Budi menjawab tidak. Ketujuh kombinasi angka 1 dan 0 tersebut ditempatkan kedalam daerah-daerah yang dipisahkan oleh tiga buah lingkaran seperti yang terlihat pada gambar berikut
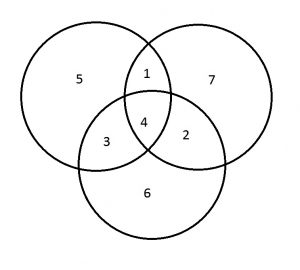
dengan bilangan 1 sampai dengan 7 menunjukkan didaerah mana angka 1 atau 0 harus ditempatkan ketika Wati mendengar jawaban Budi. Sebagai contoh, pada permainan pertama Budi menjawab ya, ya, ya, ya, tidak, tidak, ya yang berarti Wati memperoleh barisan bilangan 1,1,1,1,0,0,1 yang akan ditempatkan sesuai pada gambar di atas. Setelah ditempatkan sesuai pada tempatnya diperoleh sebagai berikut
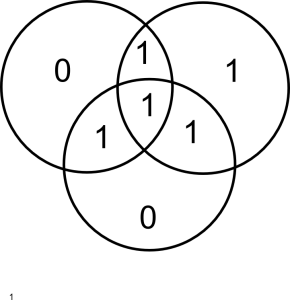
Jika Budi tidak berkata bohong, angka 1 pada setiap lingkaran muncul sebanyak genap kali. Pada gambar di atas lingkaran sebelah kanan memuat 1 sebanyak 4 kali (genap), sedangkan lingkaran kiri dan bawah muncul sebanyak ganjil kali. Ini menandakan Budi bohong pada pertanyaan yang sekaligus termuat di lingkaran kiri dan lingkaran bawah tapi tidak termuat di lingkaran kanan, yakni pertanyaan nomor 3! Dengan demikian jika Budi jujur maka Budi harus menjawab tidak pada pertanyaan ketiga sehingga angka 1 harus digantikan dengan angka 0 pada daerah untuk pertanyaan nomor 3. Sekarang untuk mengetahui bilangna Budi yang sebenarnya, Wati cukup membaca empat angka pertama pada lingkaran, yakni 1101 dan mengubahnya dari biner ke desimal untuk mendapatkan 13.
Bagaimana Metode Ini Bisa Jalan?
Misalkan Budi memberi jawaban $x_1x_2\cdots x_7$ dengan masing-masing $x_i$ bisa bernilai 0 atau 1 untuk setiap $1\leq i\leq 7$. Jika Budi tidak bohong maka berdasarkan gambar lingkaran yang paling atas, himpunan-himpunan $\{x_1,x_2,x_4,x_7\},\{x_1,x_3,x_4,x_5\},\{x_2,x_3,x_4,x_6\}$ masing-masingnya memiliki angka 1 sebanyak genap kali. Kondisi ini kita bisa tuliskan sebagai
\[\begin{align*} x_1+x_3+x_4+x_5&=0\\ x_2+x_3+x_4+x_6&=0\\ x_1+x_2+x_4+x_7&=0\end{align*}\]dimana persamaan ini kita tinjau sebagai persamaan di lapangan $\mathbb{F}_2$ yang memiliki dua unsur 0 dan 1. Ingat bahwa di $\mathbb{F}_2$ penjumlahan bersifat komutatif dan $0+0=0,0+1=1$ dan $1+1=0$.
Sistem persamaan di atas dapat kita tinjau sebagai persamaan matriks
\[\begin{align}\text{H}\begin{pmatrix}x_1\\x_2\\x_3\\x_4\\x_5\\x_6\\x_7\end{pmatrix}=0\end{align}\]dengan
\[\begin{align*}\text{H}=\begin{pmatrix}1&0&1&1&1&0&0\\0&1&1&1&0&1&0\\1&1&0&1&0&0&1\end{pmatrix}\end{align*}\]Dari sini kita lihat bahwa “himpunan jawaban jujur” adalah kernel dari $\text{H}$ dan merupakan subruang dari $\mathbb{F}_2^7$. Karena setiap ruang vektor memiliki basis, kita bisa menanyakan berapa dimensinya dan apa basisnya. Perhatikan bahwa ketiga kolom terakhir dari $\text{H}$ bebas linier. Dengan demikian $\text{rank H} =3$ dan akibatnya kernel dari $\text{H}$ berdimensi $7-3=4$.
Perhatikan bahwa matriks $\text{H}$ dapat dilihat sebagai blok-blok matriks $\text{H}=[\text{A}\mid \text{I}_3]$ untuk suatu matriks $\text{A.}$ Untuk $\text{G}=[\text{I}_4\mid -\text{A}^\text{T}]$, perhatikan bahwa
\[\begin{align*}\text{HG}^\text{T}=\text{AI}_4-\text{I}_3\text{A}=0.\end{align*}\]Dengan demikian baris-baris dari $\text{G}$ merupakan bagian dari jawaban-jawaban jujur. Akan tetapi karena
\[\begin{align*}\text{G}=\begin{pmatrix}1&0&0&0&1&0&1\\0&1&0&0&0&1&1\\0&0&1&0&1&1&0\\0&0&0&1&1&1&1\end{pmatrix}\end{align*}\]dan empat kolom pertama dari $\text{G}$ bebas linier. Dengan demikian ruang baris dari $\text{G}$, juga berdimensi 4. Ini menunjukan bahwa himpunan semua jawaban jujur adalah semua kombinasi linier dari baris-baris $\text{G}$.
Dari sini kita bisa melihat bahwa bilangan-bilangan 0 sampai dengan 15 harus kita “sandikan” sebagai unsur di ruang baris $\text{G}$ dengan tambahan syarat bahwa meskipun telah disandikan kita masih mengenalinya dengan mudah sebagai bilangan 0 sampai dengan 15. Cara yang kita lakukan sebagai berikut: untuk setiap bilangan dari 0 sampai dengan 15 tersebut, pertama kita tuliskan sebagai bilangan biner dengan panjang 4, katakan $a_1a_2a_3a_4$. Kemudian kita sandikan ia sebagai $\begin{pmatrix}a_1&a_2&a_3&a_4\end{pmatrix}\text{G}$ Sebagai contoh, untuk bilangan 5, dalam bilangan biner dengan panjang 4 ia bisa kita tuliskan sebagai $0101$. Sehingga 5 kita sandikan menjadi
Dengan melakukan hal serupa seperti di atas untuk semua bilangan 0 sampai dengan 15 kita peroleh tabel berikut:
Kemudian pertanyaan Wati yang ke-i bernilai sama dengan menanyakan apakah digit ke-i pada bilangan yang telah disandikan merupakan angka 1. Sebagai contoh pertanyaan kedua Wati senilai dengan menanyakan apakah bilangan yang telah disandikan digit keduanya 1. Dari tabel di atas kita lihat bahwa bilangan-bilangan yang digit ke-2 nya 1 adalah bilangan-bilangan di himpunan $\{4,5,6,7,12,13,14,15\}$. Dengan melakukan hal serupa untuk pertanyaan pertama sampai ketujuh maka kita peroleh semua pertanyaan Wati yang diberikan pada bagian pertama tulisan ini.
Masih ada pertanyaan yang tersisa. Darimana kita tahu bahwa dengan melakukan semua hal di atas Wati pasti selalu bisa menebak angka Budi asalkan Budi berbohong tidak lebih dari satu kali? Kita katakan dua string berjarak $k$ jika mereka berbeda di $k$ buah posisi. Jika kita lihat setiap string dengan 7 digit pada tabel di atas, setiap dua string sedikitnya berjarak 3. Sebagai contoh, string untuk 8 dan 12 yakni 1000101 dan 1100110 berjarak 3 karena mereka berbeda dalam 3 posisi, yakni pada posisi ke 2,6 dan 7. Misalkan Budi memberikan string $x$ dengan panjang 7 sebagai jawaban dari Wati. Jika Budi berbohong maka $x$ ini didapat dari suatu string $y$ dari tabel yang salah satu digitnya diubah (dari 0 ke 1 atau sebaliknya). Wati bisa menyimpulkan bahwa si $x$ ini berasal dari $y$ jika dan hanya jika $y$ adalah satu-satunya string di tabel yang berjarak 1 dari $x$. Jika ada dua string $y_1,y_2$ di tabel yang berjarak 1 terhadap $x$ maka $y_1,y_2$ paling banyak berjarak 2. Tapi ini tidak mungkin karena tadi sudah kita lihat bahwa setiap dua string di tabel berbeda sedikitnya berjarak 3!. Dari sini disimpulkan bahwa apapun angka Budi, asalkan ia tidak berbohong lebih dari satu kali, Wati pasti bisa menebaknya.
Bisa kita lihat jarak minimum memegang peranan yang sangat penting dalam solusi permasalahan ini. Secara teoretis, jika kita mempunyai himpunan yang jarak minumumnya $d$ maka Budi boleh berbohong spaling banyak $\lfloor \frac{d-1}{2}\rfloor$ kali agar Wati masih bisa menebak angka Budi. Bagaimana mengkonstruksi himpunan dengan jarak $d$ yang besar dapat dipelajari lebih lanjut di buku-buku yang membahas tentang error correcting codes.
Referensi
- Anda Boleh Berbohong Sekali! - Oleh Pak Aleams Barra (backup with archive.org)
- [Link original namun tidak berfungsi] aleamsbarra.com/2016/06/01/9/
- Teori Hamming(7,4) - Teori inti yang digunakan pada permainan